Role of Effect Size in Power Analysis
The term
"effect size" refers to the magnitude of the effect under the
alternate hypothesis. The nature of the effect size will vary from one
statistical procedure to the next (it could be the difference in cure
rates, or a standardized mean difference, or a correlation coefficient)
but its function in power analysis is the same in all procedures.
The effect
size should represent the smallest effect that would be of clinical or
substantive significance, and for this reason it will vary from one study
to the next. In clinical trials for example, the selection of an effect
size might take account of the severity of the illness being treated (a
treatment effect that reduces mortality by one percent might be clinically
important while a treatment effect that reduces transient asthma by 20%
may be of little interest). It might take account of the existence of
alternate treatments (if alternate treatments exist, a new treatment would
need to surpass these other treatments to be important). It might also
take account of the treatment's cost and side effects (a treatment that
carried these burdens would be adopted only if the treatment effect was
very substantial).
Power analysis
gives power for a specific effect size. For example, the researcher might
report "If the treatment increases the recovery rate by 20 percentage
points the study will have power of 80% to yield a significant effect".
For the same sample size and alpha, if the treatment effect is less than
20 points then power will be less than 80%. If the true effect size exceeds
20 points, then power will exceed 80%.
 While
one might be tempted to set the "clinically significant effect"
at a small value to ensure high power for even a small effect, this determination
cannot be made in isolation. The selection of an effect size reflects
the need for balance between the size of the effect that we can detect,
and the resources available for the study.
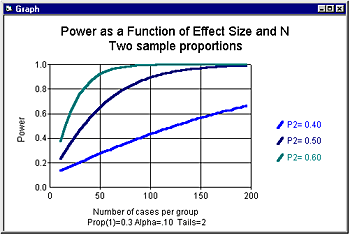
Small effects will require a larger investment of resources than large
effects. Figure 1 shows power as a function of sample size for three levels
of effect size (assuming alpha, 2-tailed, is set at .05). For the smallest
effect (30% vs. 40%) we would need a sample of 356 per group to yield
power of 80%. For the intermediate effect (30% vs. 50%) we would need
a sample of 93 per group to yield this level of power. For the highest
effect size (30% vs. 60%) we would need a sample of 42 per group to yield
power of 80%. We may decide that it would make sense to enroll 93 per
group to detect the intermediate effect but inappropriate to enroll 356
patients per group to detect the smallest effect.
The "true"
(population) effect size is not known. While the effect size in the power
analysis is assumed to reflect the population effect size for the purpose
of calculations, the power analysis is more appropriately expressed as
"If the true effect is this large power would be ... " rather
than "The true effect is this large, and therefore power is ..."
This distinction
is an important one. Researchers sometimes assume that a power analysis
cannot be performed in the absence of pilot data. In fact, it is usually
possible to perform a power analysis based entirely on a logical assessment
of what constitutes a clinically (or theoretically) important effect.
Indeed, while the effect observed in prior studies might help to provide
an estimate of the true effect it is not likely to be the true effect
in the population - if we knew that the effect size in these studies was
accurate, there would be no need to run the new study.
Since the
effect size used in power analysis is not the "true" population
value, the researcher may elect to present a range of power estimates.
For example (assuming N=93 per group and alpha=.05, 2 tailed), "The
study will have power of 80% to detect a treatment effect of 20 points
(30% vs. 50%), and power of 99% to detect a treatment effect of 30 points
(30% vs. 50%)".
Cohen has
suggested "conventional" values for "small", "medium"
and "large" effects in the social sciences. The researcher may
want to use these values as a kind of reality-check, to ensure that the
values he/she has specified make sense relative to these anchors. The
program also allows the user to work directly with one of the conventional
values rather than specifying an effect size, but it is preferable to
specify an effect based on the criteria outlined above, rather than relying
on conventions.
Previous | Next
| 
