Role of Sample Size - Precision

The confidence interval represents the precision with which we are able to report the effect size, and the larger the sample, the more precise the estimate. As a practical matter, sample size is often the dominant factor in determining the precision.

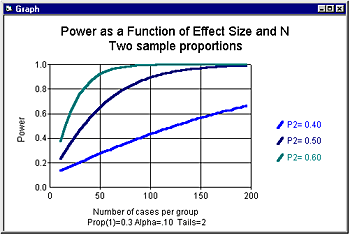Figure 3 shows precision for a rate difference as a function of sample size. This figure is based on the same rates used in the Power analysis (30% vs. 50%). With N=50 per group the effect would be reported as 20 points with 95% confidence interval of plus/minus some 19 points (01 to 39 points). With N=100 per group the effect would be reported as 20 points with 95% confidence interval of plus/minus some 13 points (7 to 33). With N=200 per group the effect would be reported as 20 points with 95% confidence interval of plus/minus some 9 points (11 to 29).

Note: For studies that involve two groups precision is maximized when the subjects are divided evenly between the two groups (this statement applies to the procedures included in this program). When the number of cases in the two groups is uneven the "effective N" for computing precision falls much closer to the smaller sample size than the larger one.

Precision - Role of Confidence Level

The confidence level is an index of certainty. For example (With N=93 per group) we might report that the treatment improves the response rate by 20 percentage points, with a 95% confidence interval of plus/minus some 13 points (7 to 33). This means that in 95% of all possible studies, the confidence interval computed in this manner will include the true effect. The confidence level is typically set in the range of 99% to 80%.

The 95% confidence interval will be wider than the 90% interval, which in turn will be wider than the 80% interval. For example, compare Figure 4, which shows the expected value of the 80% confidence interval, with Figure 3 which is based on the 95% confidence interval. With a sample of 100 cases per group the 80% confidence interval is plus/minus some 9 points (11 to 29) while the 95% confidence interval is plus/minus some 13 points (7 to 34).

The researcher may elect to report the confidence interval for more than one level of confidence, for example "The treatment improves the cure rate by 10 points (80% confidence interval 11 to 29, and 95% confidence interval 7 to 34. It has also been suggested that the researcher use a graph to report the full continuum of confidence intervals by as a function of confidence levels. (See Poole, 1987a,b,c; Walker, 1986a,b)

Precision - Role of Tails

The researcher may elect to compute two-tailed or one-tailed bounds for the confidence "interval". A two-tailed confidence interval extends from some finite value below the observed effect to another finite value above the observed effect. A one-tailed confidence "interval" extends from minus infinity to some value above the observed effect, or from some value below the observed effect to plus infinity (the logic of the procedure may impose a limit other than infinity, such as 0 and 1 for proportions). A one-tailed confidence interval might be used if were concerned only with effects in one direction. For example, we might report that a drug increases the remission rate by 20 points with a 95% lower limit of 15 points (the upper limit is of no interest).

For any given sample size, dispersion and confidence level, a one-tailed confidence "interval" is "narrower" than a two tailed interval in the sense that the distance from the observed effect to the computed boundary is smaller for the one-tailed interval (the one-tailed case is not really an interval, since it has only one boundary). As was the case with power analysis, however, the decision to work with a one-tailed procedure rather than a two-tailed procedure should be made on substantive grounds, rather than as a means for yielding a more precise estimate of the effect size.

Role of effect size variance in Precision

The third element determining precision is the dispersion of the effect size index. For t-tests, dispersion is indexed by the standard deviation of the group means. If we will be reporting precision using the metric of the original scores, then precision will vary as a function of the SD. (If we will be reporting precision using a standard index, then the SD is assumed to be 1.0 and so the SD of the original metric is irrelevant.) For tests of proportions the variance of the index is a function of the proportions. Variance is highest for proportions near .50 and lower for proportions near 0.0 or 1.0. As a practical matter, variance is fairly stable until proportions fall below .10 or above .90). For tests of correlations the variance of the index is a function of the correlation. Variance is highest when the correlation is zero.

Role of effect size in Precision

Effect size, which is a primary factor in computation of power, has little (if any) impact in determining precision. In the running example we would report a 20 point effect with a 95% confidence interval of plus/minus some 13 points. A 30 point effect would similarly be reported with a 95% confidence interval of plus/minus some 13 points.

While effect size plays no direct role in precision, it may be related to precision indirectly. Specifically, for procedures that work with mean differences, the effect size is a function of the mean difference and also the SD within groups. The former has no impact on precision; the latter affects both effect size and precision (a smaller SD yields higher power and better precision in the raw metric). For procedures that work with proportions or correlations the absolute value of the proportion or correlation affects the index's variance, which in turn may have an impact on precision.

Precision - Controlling

The process of planning for precision has some obvious parallels to planning for power, but the two processes are not identical and, in most cases, will lead to very different estimates for sample size. The program displays an estimate of the precision for a given sample size and confidence level.

Typically, the user will enter data for effect size and sample size. The program immediately displays both power and precision for the given values. Changes to effect size will affect power (and may have an incidental effect on precision). Changes to sample size will affect both power and precision. Changes to alpha will affect power, while changes to the confidence level will affect precision. Defining the test as one-tailed or two-tailed will affect both power and precision.

Precision - Tolerance intervals

The confidence interval width displayed for t-tests is the median interval width (assuming the population SD is correct, the confidence interval will be narrower than the displayed value in half the samples, and wider in half the samples). The width displayed for exact tests of exact proportions is the expected value (i.e. the mean width expected over an infinite number of samples). For other procedures where the program displays a confidence interval, the width shown is an approximate value (it is the value that would be computed if the sample proportions or the sample correlation precisely matched the population values).

For many applications, especially when the sample size is large, these values will prove accurate enough for planning purposes. Note, however, that for any single study the precision will vary somewhat from the displayed value. For t-tests, on the assumption that the population SD is 10, the sample SD will typically be smaller or greater than 10, yielding a narrower or wider confidence interval. Analogous issues exist for tests of proportions or correlations.

For t-tests the researcher who requires more definitive information about the confidence interval may want to compute tolerance intervals, i.e. the likelihood that the confidence interval will be no wider than some specific value. In this program the 50% tolerance interval (corresponding to the median value) is displayed as a matter of course. The 80% (or other user-specified) tolerance interval is an option enabled from the View menu. For example, the researcher might report that in 50% of all studies the mean would be reported with a 95% confidence interval no wider than 9 points, and in 80% of all studies the mean would be reported with a 95% confidence interval no wider than 10 points.

Note. The confidence interval displayed by the program is intended for anticipating the width of the confidence interval while planning a study, and not for computing the confidence interval after a study is completed. The computational algorithm used for t-tests includes an adjustment for the sampling distribution of the SD that is appropriate for planning but not for analysis. The computational algorithms used for tests of proportions or a single correlation may be used for analysis as well.